一道经典的分治

题目链接

题意是套圈游戏要设计一款尺寸最大的圆环，满足圆环不会一次套中两个物品。每个物品有一个摆放坐标。我们要求的是这些物品中相邻最近的两个物品之间的距离，这个距离就是我们要求的圆环的直径。

这个类型网上常称为寻找最近点对问题。

数据是十万（1e5），分治算法时间复杂度是O(nlogn)，刚好能够跑完。

分治的思想就是我们先将所有点按照横坐标从小到大排序，然后将点分成左右两部分，也就是图中的L和R区域，这样我们就可以分别求两边的距离最小值。当然在中间线的mid部分也是需要求距离的。

在算完两边的距离最小值d后，我们将中间线向左和向右扩展d长度，组成mid的领域。可以知道如果领域再扩大增加的点并不会形成更优的答案。这里需要注意，我们的L和R区域是以中间线为界，也就是说mid区域其实是叠加在两边区域之上的。

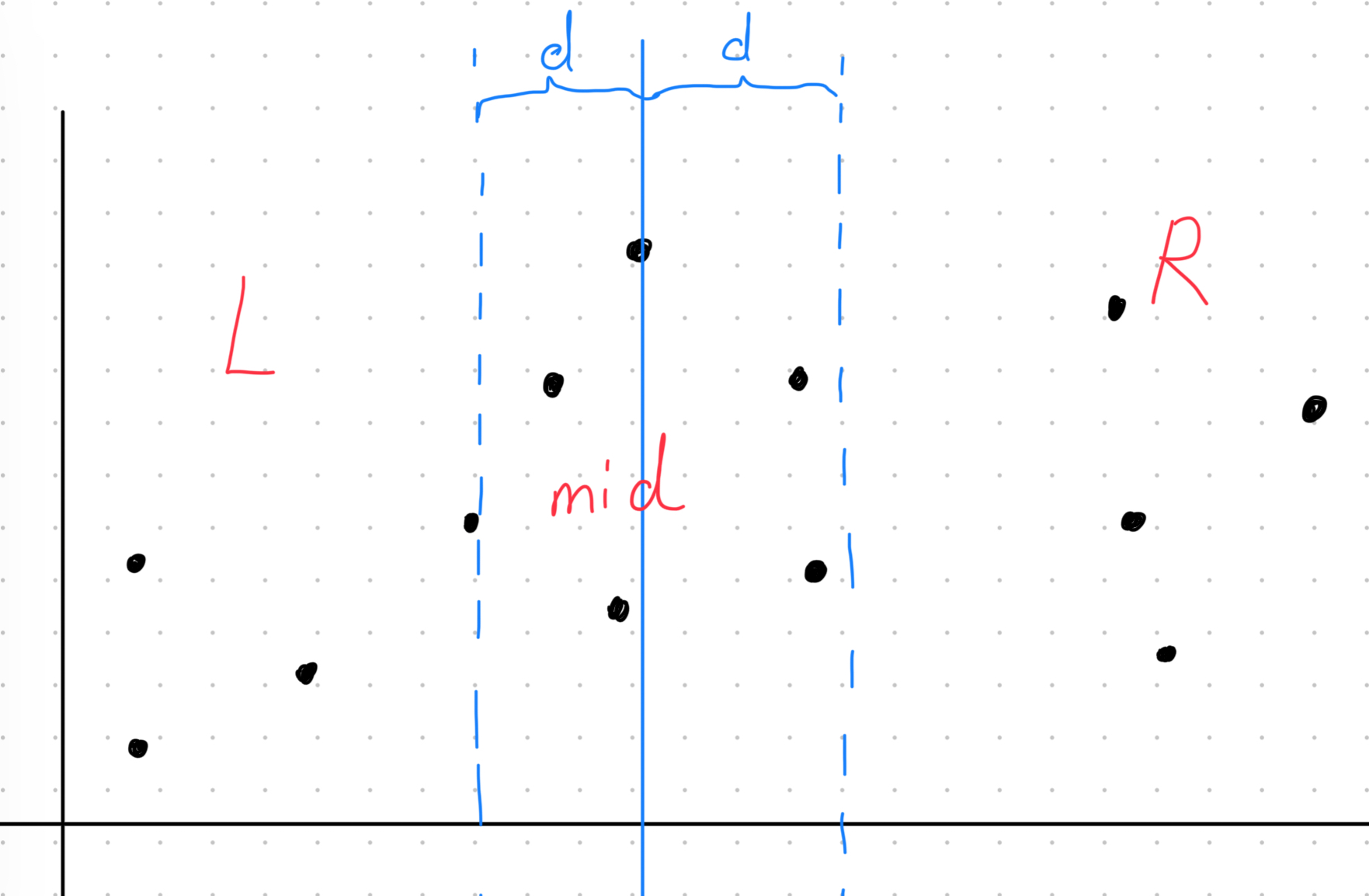
fenzhi

虽然中间区域的点已经会排除掉一些点，但是直接用双重循环找最短距离会超时。这是因为如果点都在中间密集的话时间复杂度会接近O(n*n)。

所以我们需要把中间点按照y的从小到大排序，在循环中如果两点纵坐标之间的距离已经大于d的时候及时跳出循环，完成剪枝。在oi-wiki中有证明，这里的满足条件的点不会超过7。

边界问题：自己与自己之间距离设置成足够大的值，如果区间只有两个点，则直接计算两点之间距离。

PS: 函数命名不要用distance，会和C++库中函数重名而导致CE

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<iostream>
#include<cstdio>
#include<map>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;

const int mxlen = 1e5+5;
struct node{
    double x;
    double y;
}points[mxlen];
// sort by x
bool cmpx(node qw,node er){
    if(qw.x==er.x) return qw.y<er.y;
    return qw.x<er.x;
    
}

// sort by y
bool cmpy(node qw,node er){
    if(qw.y==er.y) return qw.x<er.x;
    return qw.y<er.y;
}
// count the distance between two points
// name can not be distance, because there is a function named distance in cmath
double dis(node qw,node er){
    return sqrt((qw.x-er.x)*(qw.x-er.x)+(qw.y-er.y)*(qw.y-er.y));
}  

int n;
node temp[mxlen];
double solve(int l,int r){
    if(l==r) return 1e20;
    // if there are only two points
    if(l+1==r) return dis(points[l],points[r]);
    int mid = (l+r)>>1;
    double d = min(solve(l,mid),solve(mid+1,r));

    // sort by y, otherwise the code will TLE
    int len = 1;
    for(int i=mid;i>=l&&points[mid].x-points[i].x<d;i--) temp[len++] = points[i];
    for(int i=mid+1;i<=r&&points[i].x-points[mid].x<d;i++) temp[len++] = points[i];
    sort(temp+1,temp+len,cmpy);
    for(int i=1;i<len;i++){
        for(int j=i+1;j<len&&temp[j].y-temp[i].y<d;j++){
            d = min(d,dis(temp[i],temp[j]));
        }
    }
    return d;
}
int main(){
    while(1){
        scanf("%d",&n);
        if(!n) break;
        for(int i=1;i<=n;i++){
            scanf("%lf%lf",&points[i].x,&points[i].y);
        }
        sort(points+1,points+n+1,cmpx);
        double ans = solve(1,n);
        printf("%.2f\n",ans/2);
    }
    return 0;
}