细心和智慧并存的解答

题目链接

题的大致意思是能不能从起点经过T时间精准到达终点，图中有一些障碍不能走，走过的格子也不能再走。

其中数据是最大7*7的迷宫，最多50个迷宫。

智慧之处——精准的剪枝

类似全排列的深搜时间复杂度是O(n!)，7*7的数据是过不去的。

首先就是普通地剪枝：

  • 如果时间已经大于T，就不用再走了
  • 如果已经有正确答案，要及时地退出搜索

然后是奇偶剪枝，这里参考了其他博客

这里我重新画了一张图，如下：

maze

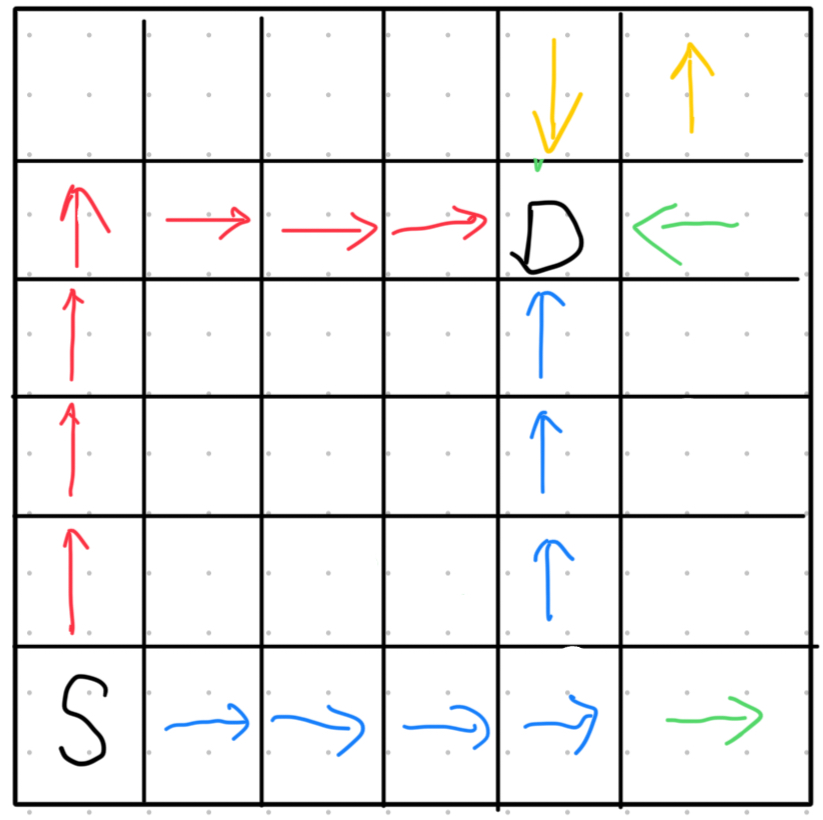
图中的S可以代表任何你走到的位置，不一定是起点。就如图中的红色和蓝色路径，这两条路径是最少需要的时间。如果剩余时间少于最短路径长度，那么是一定不能到达终点的。

既然时间不够一定不能到达，时间刚好和剩余最少时间相等也能到达，那么还剩一种情况，就是时间大于剩余最少时间。这也应该是大概率会遇到的情况。根据题意我们只能在第T秒精准到达终点，我们时间多出来的怎么办呢？——我们需要在终点周围“徘徊”。

如图中的绿色和黄色箭头所示，你比最短路径多走出来的路径，一定是先“出去”，再“回来”。多走的路径是“对称的”，那多出来的路径长度一定是偶数。

这就是奇偶性剪枝。加上这个剪枝就能过所有的测试数据。

细心之处——多数据下数组的重复利用

尽管我写过无数个全排列暴力骗过不少10分、20分。但是在这道题上还是因为粗心而浪费了不少时间。

在做杭电这前十道题的时候我就发现基本都是多数据的形式。所以除了输入会重新填入数据的数组外，其他数据都需要进行“初始化”。

但是即使我清空了vis数据，我发现代码运行的答案竟然是错误的（样例是能过的）。

原因就是这道题毕竟不是全排列，vis数组不能只在dfs的for循环中去设置。你的起点在你走出第一步后就再也不能回来了。

vis[startX][startY]=true;

代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<iostream>
#include<cstdio>
#include<map>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;

char mp[10][10];
int n,m,T;
bool vis[10][10];

int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};

string ans;

int startX,startY,endX,endY;
void dfs(int x,int y,int step){
    if(ans=="YES") return;
    else if(step>T) return;
    else if(mp[x][y]=='D'&&step==T){
        ans = "YES";
        return;
    }

    // 剩余时间小于到终点的最短距离
    if(T-step<(abs(x-endX)+abs(y-endY))){
        return;
    }
    // 剩余时间剪去最短距离不是偶数
    if((T-step-(abs(x-endX)+abs(y-endY)))%2!=0){
        return;
    }
    for(int i=0;i<4;i++){
        int nx = x+dx[i];
        int ny = y+dy[i];
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[nx][ny]&&mp[nx][ny]!='X'){
            vis[nx][ny]=true;
            dfs(nx,ny,step+1);
            vis[nx][ny]=false;
        }
    }
}
int main(){
    while(1){
        scanf("%d%d%d",&n,&m,&T);
        if(!n&&!m&&!T) break;
        
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                cin>>mp[i][j];
                if(mp[i][j]=='S'){
                    startX=i;
                    startY=j;
                }else if(mp[i][j]=='D'){
                    endX=i;
                    endY=j;
                }
            }
        }
        ans = "NO";
        // vis记得清空
        memset(vis,false,sizeof(vis));
        // 起点要标记为已访问 
        vis[startX][startY]=true;
        dfs(startX,startY,0);
        cout<<ans<<endl;
    }
    return 0;
}