Notes of Lecture 23: Computational Complexity
Notes of Lecture 23: Computational Complexity
P,EXP,R
P = {problems solvable in at most(<=) polynomial time}
EXP = {problems solvable in exponential(2^$n^c$) time}
R = {problems solvable in finite time}
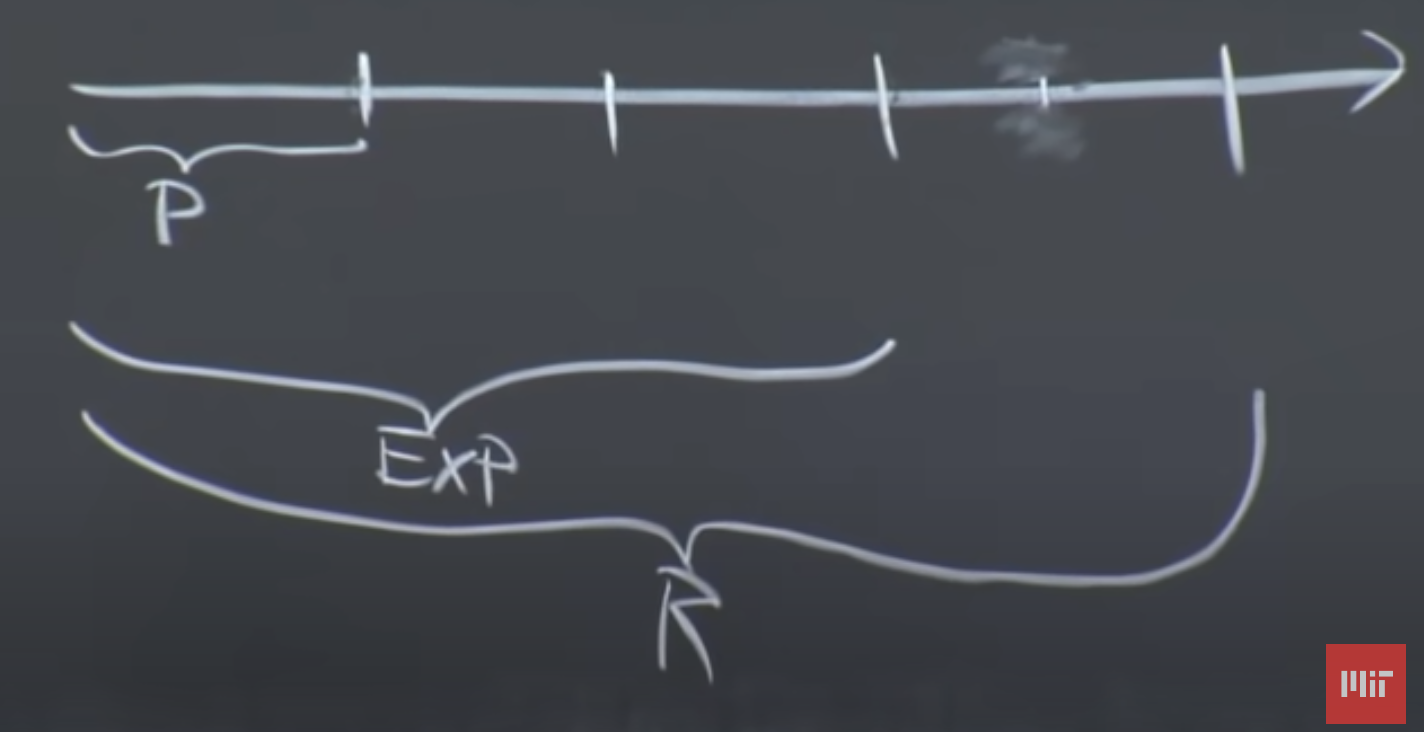
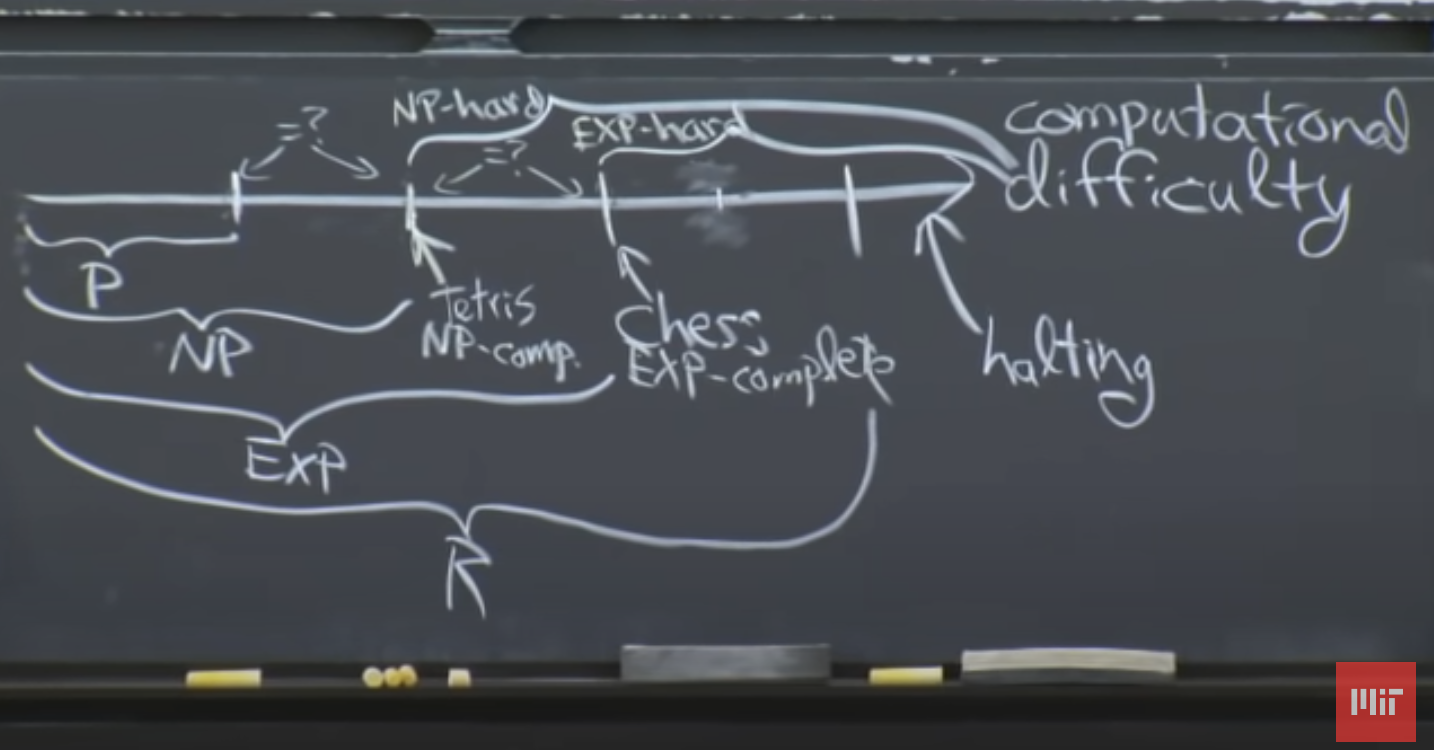
The axis is computational difficulty.
Most problems uncomputable
Examples:
- negative-weight cycle detection (P)
- NxN Chess (EXP&!P)
- Tetris (EXP, don’t know whether is P)
- halting problem: given program, does it ever halt/stop? (not in R)
Most decision problems are uncomputable (not in R)
- program $\approx$ binary string $\approx$ natural number (integer)
- decision problem = function : input($\approx$ binary string (N)) ->{yes(1),no(0)}
So decision problem is in $\mathbb{R}$;
$|\mathbb{R}|$ >> $|\mathbb{N}|$ => almost every problem unsolvable by any program
NP
NP = {decision problems solvable in polynomial time via a “lucky” algorithm}
nondeterministic model : algorithm makes guesses & says YES/NO.
guesses are guaranteed to lead to “YES” if possible
Tetris is NP
proof = sequence of moves to make
NP = {decision problems with “solutions” that can be “checked” in polynomial time}
- When answer = YES, can prove it & check proof in polynomial time.
Hardness & Completeness
P!=NP : big conjecture $\approx$ “can’t engineer luck” $\approx$ generating (proofs of) solutions can be harder than checking them.
Claim: if P!=NP then Tetris is NP-P => not in P.
Why? Tetris is NP-hard(as hard as every problem which is NP)
- in fact Tetris is NP-complete = NP $\cap$ NP-hard
Reductions
Reductions: A -> B
convert problem A(don’t know how to solve) into problem B(you know how to solve)
unweighted shortest paths -> weighted shortest paths
min-product path -> shortest path
longest path -> shortest path
B is as hard ad A
3- partition [Karp] -> Tetris





