Derangement Problem

problem link

Problem Description

You have n letters, each with a different recipient. However, all the letters are delivered to the wrong recipients, meaning no one receives the letter intended for them. You need to determine how many possible ways this can happen.

This problem can be simplified to a case where you have an array of numbers from 1 to n. For each position in the array(starting from index 1), the number in that position is different from its index. The goal is to count how many such arrangement exist.

Algorithm

This is a classic derangement problem. You can find a more detailed explanation on oi-wiki and wikipedia.

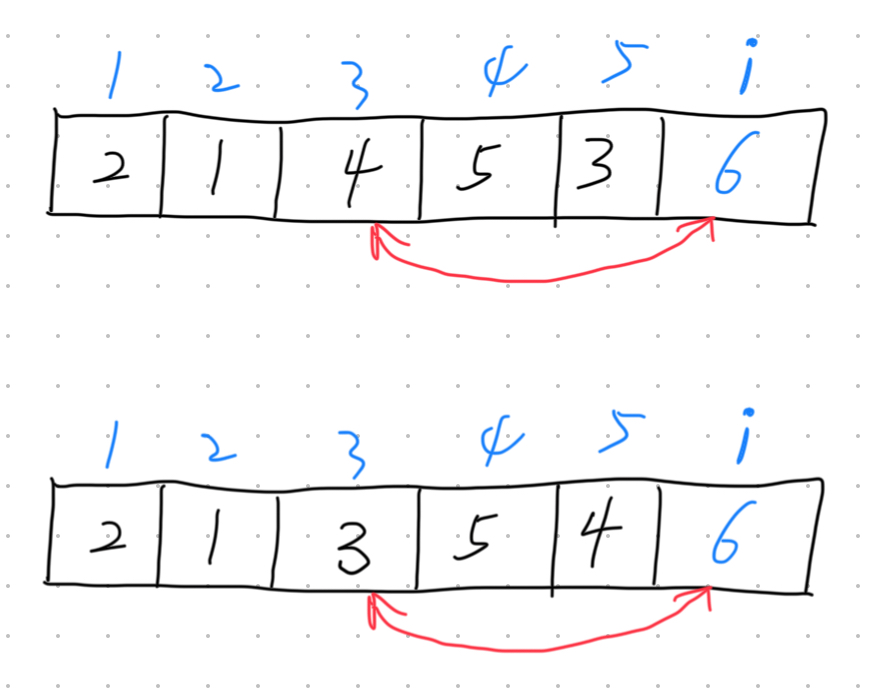
I solved the problem using a recursive approach. LetD[i]represent the number of derangements when n = i. The recursive formula is: D[i]=(i-1)D[i-1]+(i-1)D[i-2].

Here’s an explanation of the formula:

Assume we already know the answers for i-1. Now, we add the i-th number to the sequence in the i-th position. Since the number in each position must differ from the position itself, we need to swap i with a number in the previous positions. The first case is where all of the previous i-1 numbers are already deranged, so we can swap i with any of them, giving us (i-1)D[i-1] possibilities. The second case is where i-2 numbers are deranged, but one number matches its index. In this case, we swap i with that number, which gives us (i-1)D[i-2] possibilities.

dislocation

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<cstdio>
#include<map>
#include<cmath>
#include<string>
#include<algorithm>
#include<iomanip>
#define ll long long
using namespace std;
ll a[25];
void init(){
    a[2] = 1;
    a[3] = 2;
    for(int i=4;i<=20;i++){
        a[i] = (i-1)*(a[i-1]+a[i-2]);
    }
}
int main(){
    init();
    int n;
    while(scanf("%d",&n)!=EOF){
        printf("%lld\n",a[n]);
    }
    return 0;
}