M子段和最大问题

Problem Link

Given an array and divide into m sequences. One sequences at least has one number and the sequences can’t contain the number with same index. And the index of the numbers in one sequence should be continuous. Notice that we don’t have to use all the numbers.

N between 1 to 1e6.

SOLUTION

Dynamic programming.

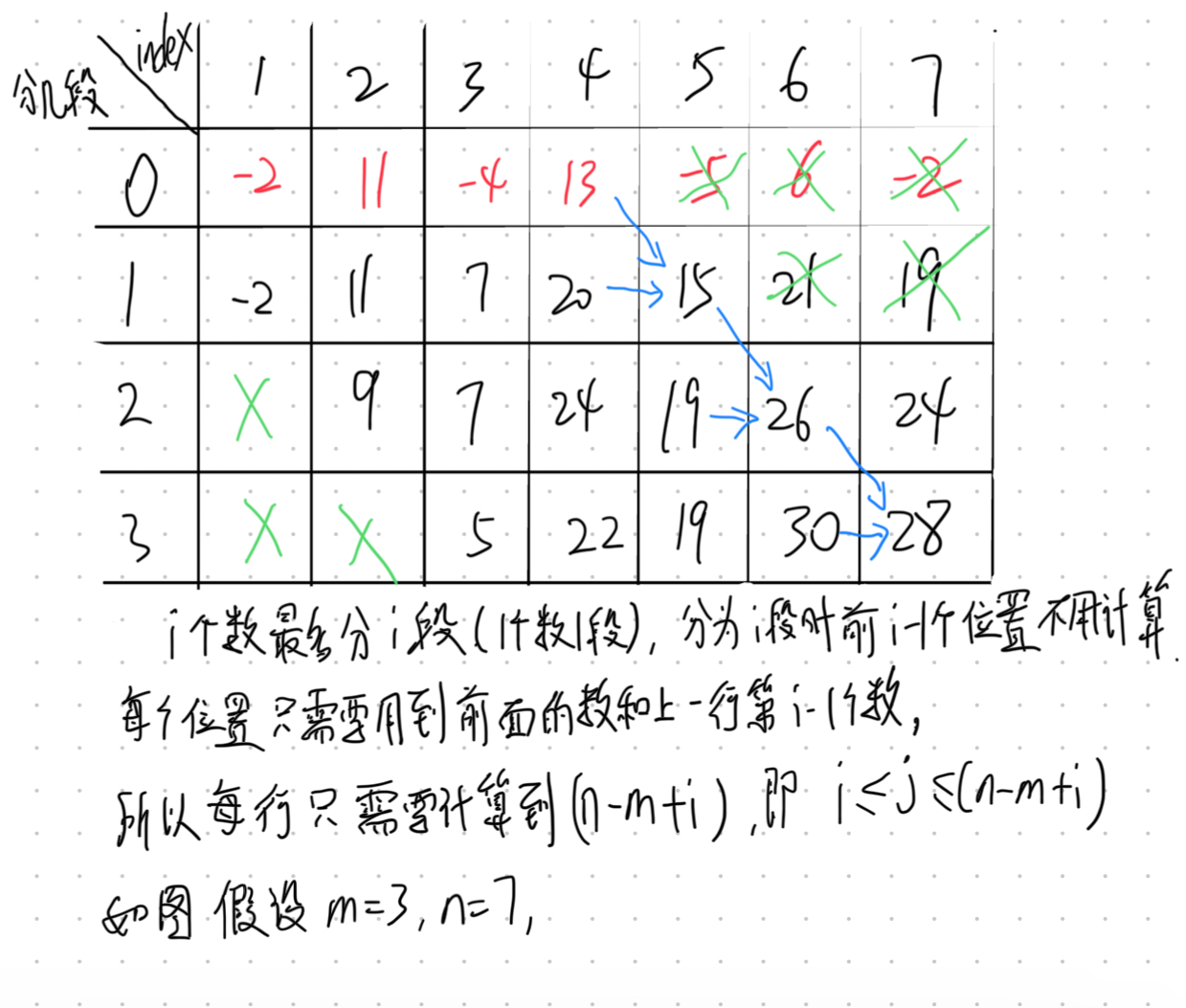
Let d[i][j] denote the maximum sum of the current array that is divided into i segments and the last segment ends with the jth number.

When comes to the jth number, we have two options. One is the jth number to be a new segments, the other is to add it to the back of the last segment which ends with (j-1)th number.

So the transfer equation is dp[i][j]=max(pre_max+a[j],dp[i][j-1]+a[j]). pre_max represents to the maximum answer that the pre array divided into i-1 segments.

Reference blog

Reference Image

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
#include<cstdio>
#include<map>
#include<cmath>
#include<queue>
#include<string>
#include<algorithm>
#include<iomanip>
#define ll long long
using namespace std;
const int mxlen = 1e6+5;
const int inf = 0x3f3f3f3f;
int n,m;
ll dp[mxlen];
ll a[mxlen];
int main(){
    while(scanf("%d%d",&m,&n)!=EOF){
        // 用memset会超时
        //memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++) {
            scanf("%lld",&a[i]);
            dp[i] = 0;
        }
        for(int i=1;i<=m;i++){
            ll pre = dp[i-1];
            ll pre_max = -inf;
            for(int j=i;j<=n-m+i;j++){
                pre_max = max(pre_max,pre);
                pre = dp[j];
                if(j!=i) dp[j] = max(pre_max,dp[j-1])+a[j];
                else dp[j] = pre_max+a[j];
            }
        }
        ll ans = -inf;
        for(int i=m;i<=n;i++){
            ans = max(ans,dp[i]);
        }
        printf("%lld\n",ans);
    }
    return 0;
}