AiRomance

HDU 4870 概率DPProblem Link 题意新账号打rank，rank从0开始，打到1000分结束。每场rank增加50的概率为p，否则rank-100。新人用两个信号去打，每次用rank值低的账号，问任意一个账号达到rank1000分，新人要打的期望场数。 解答参考博客 将分数离散为赢了加1分，输了减2分。用dp[i]表示从i-1分到i分需要打的期望场数。 每次比赛有两种情况，一是p概率赢了加1分，二是(1-p)概率输了减2分。 dp[i]=1*p+(1-p)(1+dp[i-2]+dp[i-1]+dp[i]) 期望等于所有情况乘以概率的和。 一场就赢了，则是1*p 一场输了，则需要(1+dp[i-2]+dp[i-1]+dp[i])场才能赢回来。其中1是输了这场，然后从i-3打到i-2,从i-2打到i-1，从i-1打到i分。 化简得 dp[i]=(1+(1-p)*(dp[i-2]+dp[i-1]))/p dp[1] = 1/p, dp[2] =...

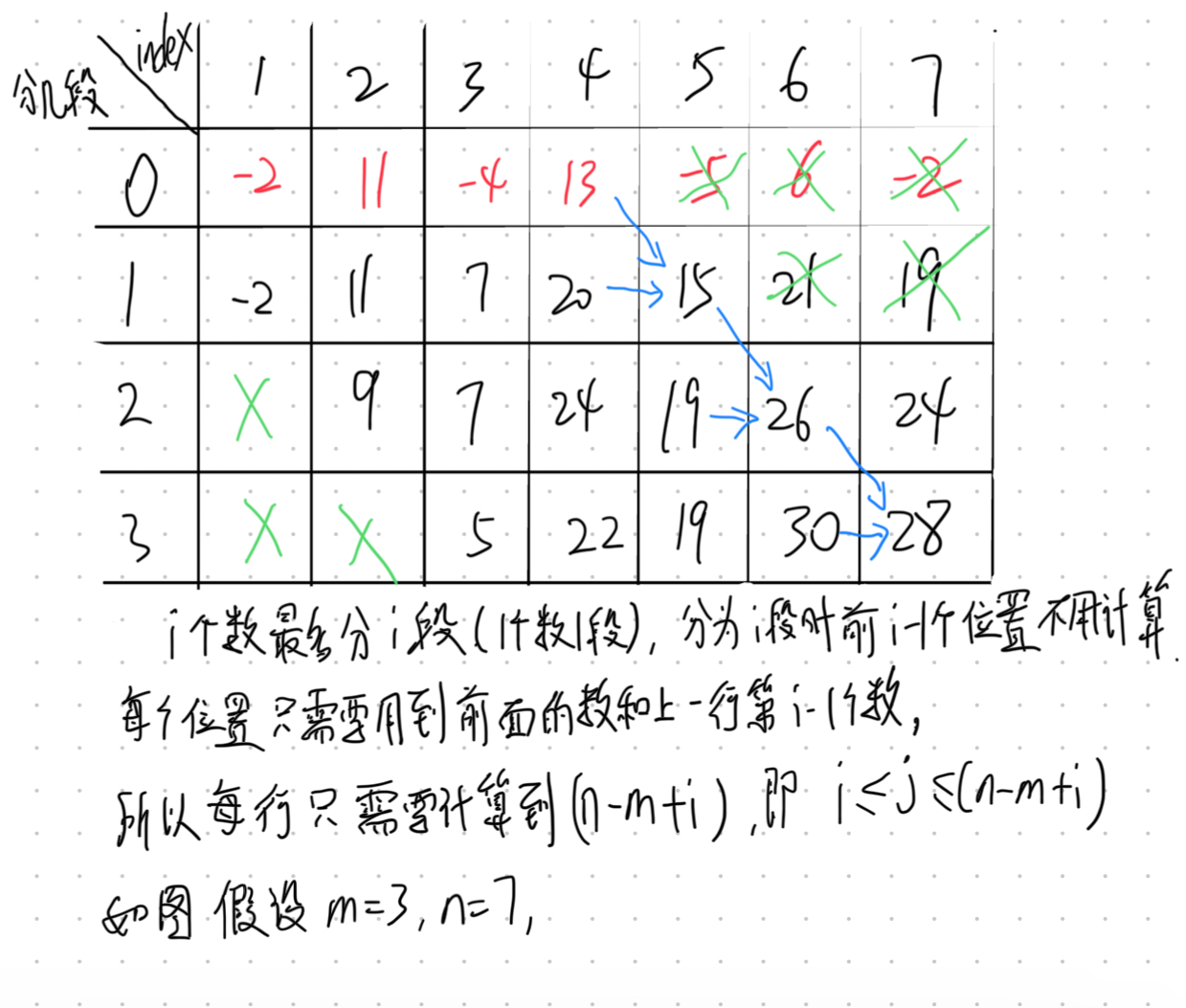
M子段和最大问题Problem Link Given an array and divide into m sequences. One sequences at least has one number and the sequences can’t contain the number with same index. And the index of the numbers in one sequence should be continuous. Notice that we don’t have to use all the numbers. N between 1 to 1e6. SOLUTIONDynamic programming. Let d[i][j] denote the maximum sum of the current array that is divided into i segments and the last segment ends with the jth number. When comes to the jth number,...

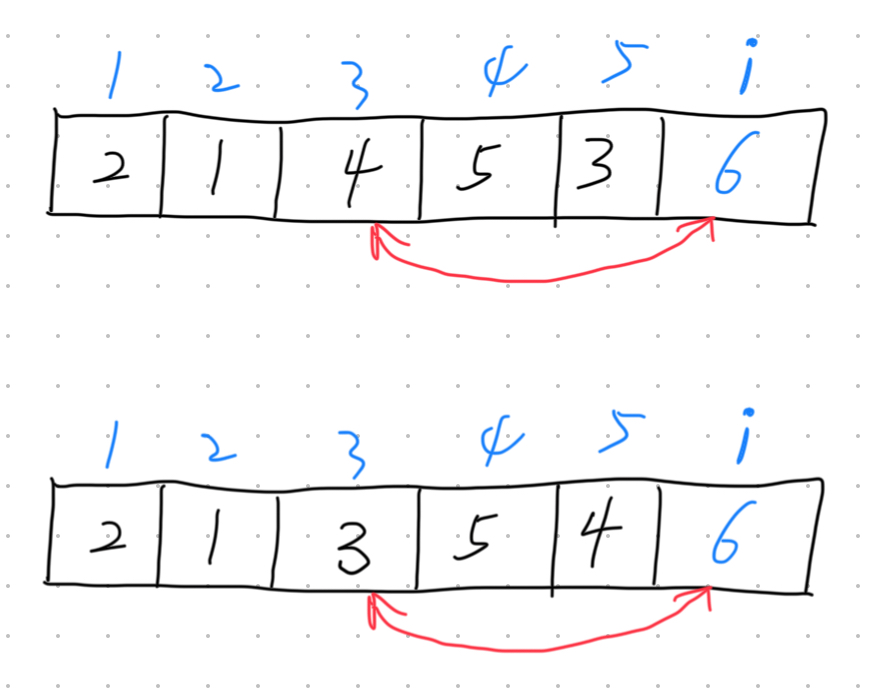
寻找数列主元素Problem link Finding a integer that appears at least (N+1)/2 times in the array. 摩尔投票法The Boyer-Moore Voting Algorithm (Moore’s Voting Algorithm) is a highly efficient method to find the majority element in a sequence (an element that appears more than half the time). It operates in O(n) time and uses O(1) space. Key Idea:The algorithm works by maintaining a candidate for the majority element and a counter to track its occurrences. It leverages a “pairing” or “cancellation” mechanism...

Derangement Problemproblem link Problem DescriptionYou have n letters, each with a different recipient. However, all the letters are delivered to the wrong recipients, meaning no one receives the letter intended for them. You need to determine how many possible ways this can happen. This problem can be simplified to a case where you have an array of numbers from 1 to n. For each position in the array(starting from index 1), the number in that position is different from its index. The goal is...

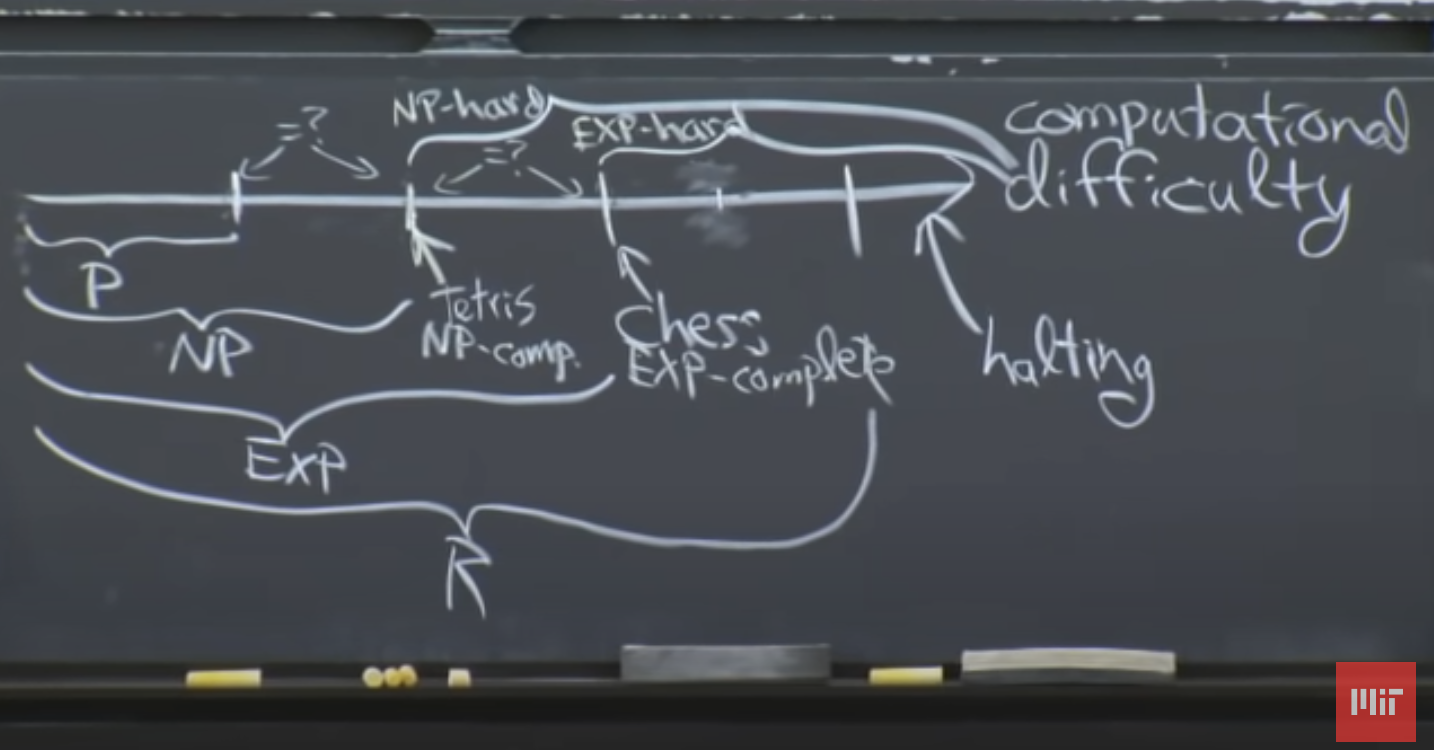
Notes of Lecture 23: Computational Complexityvideo link P,EXP,RP = {problems solvable in at most(<=) polynomial time} EXP = {problems solvable in exponential(2^$n^c$) time} R = {problems solvable in finite time} The axis is computational difficulty. Most problems uncomputableExamples: negative-weight cycle detection (P) NxN Chess (EXP&!P) Tetris (EXP, don’t know whether is P) halting problem: given program, does it ever halt/stop? (not in R) Most decision problems are uncomputable...

Multiple Knapsack Problemproblem link The Meaning of the problemYou have three kinds of coins. Their face values are 1,2 and 5. Of cause you only have a limited number of coins. You need to find the minimum value that you can’t represent exactly with these coins. SolutionThere are lots of people solve this problem using Generating function. That way is too hard to understand. We just need to think of this problem as a multiple knapsack problem. I learned from this blog dp[j] = 1 means that...

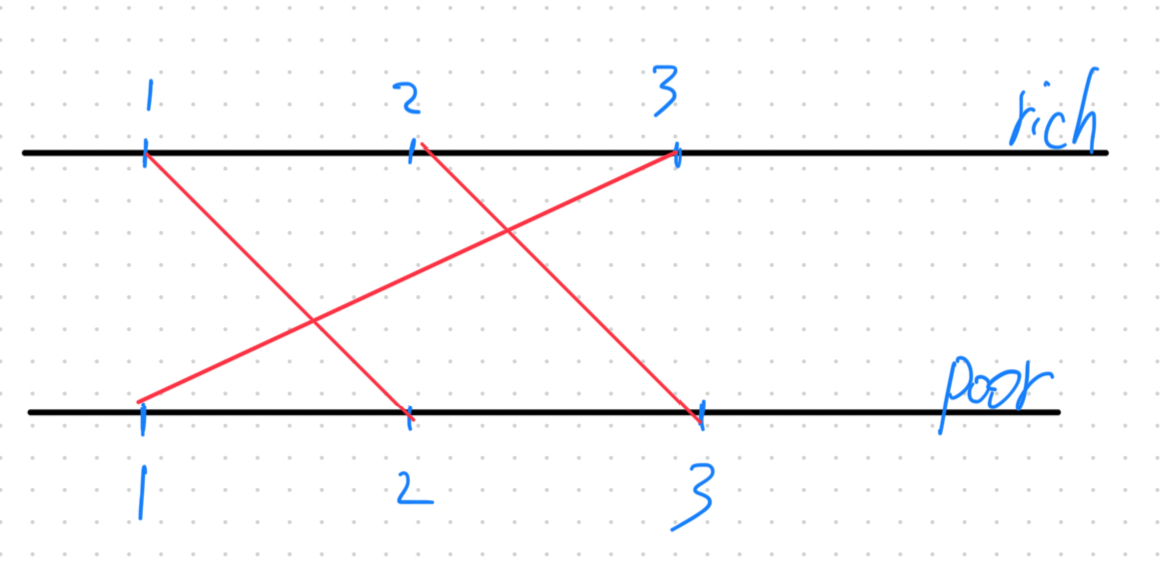
Constructing Roads In JGShining’s Kingdomproblem link The meaning of the problemSo why this is longest increasing subsequence Problem ? Look at the picture below: As the problem described, we can’t have crossed lines. Each line has two endpoints. One is the “rich” endpoint above and the other is the “poor” endpoint below. The rich endpoints’ number of the lines we finally pick up should be monotonically increasing. The corresponding poor endpoints should be monotonically increasing too....

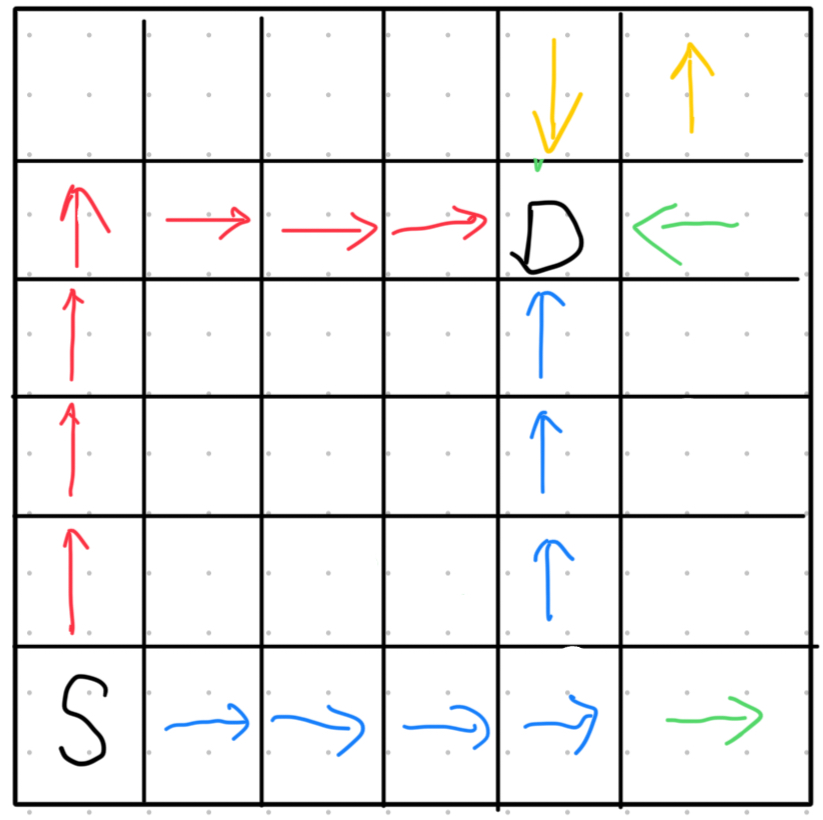
细心和智慧并存的解答题目链接 题的大致意思是能不能从起点经过T时间精准到达终点，图中有一些障碍不能走，走过的格子也不能再走。 其中数据是最大7*7的迷宫，最多50个迷宫。 智慧之处——精准的剪枝类似全排列的深搜时间复杂度是O(n!)，7*7的数据是过不去的。 首先就是普通地剪枝： 如果时间已经大于T，就不用再走了 如果已经有正确答案，要及时地退出搜索 然后是奇偶剪枝，这里参考了其他博客 这里我重新画了一张图，如下： 图中的S可以代表任何你走到的位置，不一定是起点。就如图中的红色和蓝色路径，这两条路径是最少需要的时间。如果剩余时间少于最短路径长度，那么是一定不能到达终点的。 既然时间不够一定不能到达，时间刚好和剩余最少时间相等也能到达，那么还剩一种情况，就是时间大于剩余最少时间。这也应该是大概率会遇到的情况。根据题意我们只能在第T秒精准到达终点，我们时间多出来的怎么办呢？——我们需要在终点周围“徘徊”。 如图中的绿色和黄色箭头所示，你比最短路径多走出来的路径，一定是先“出去”，再“回来”。多走的路径是“对称的”，那多出来的路径长度一定是偶数。 ...

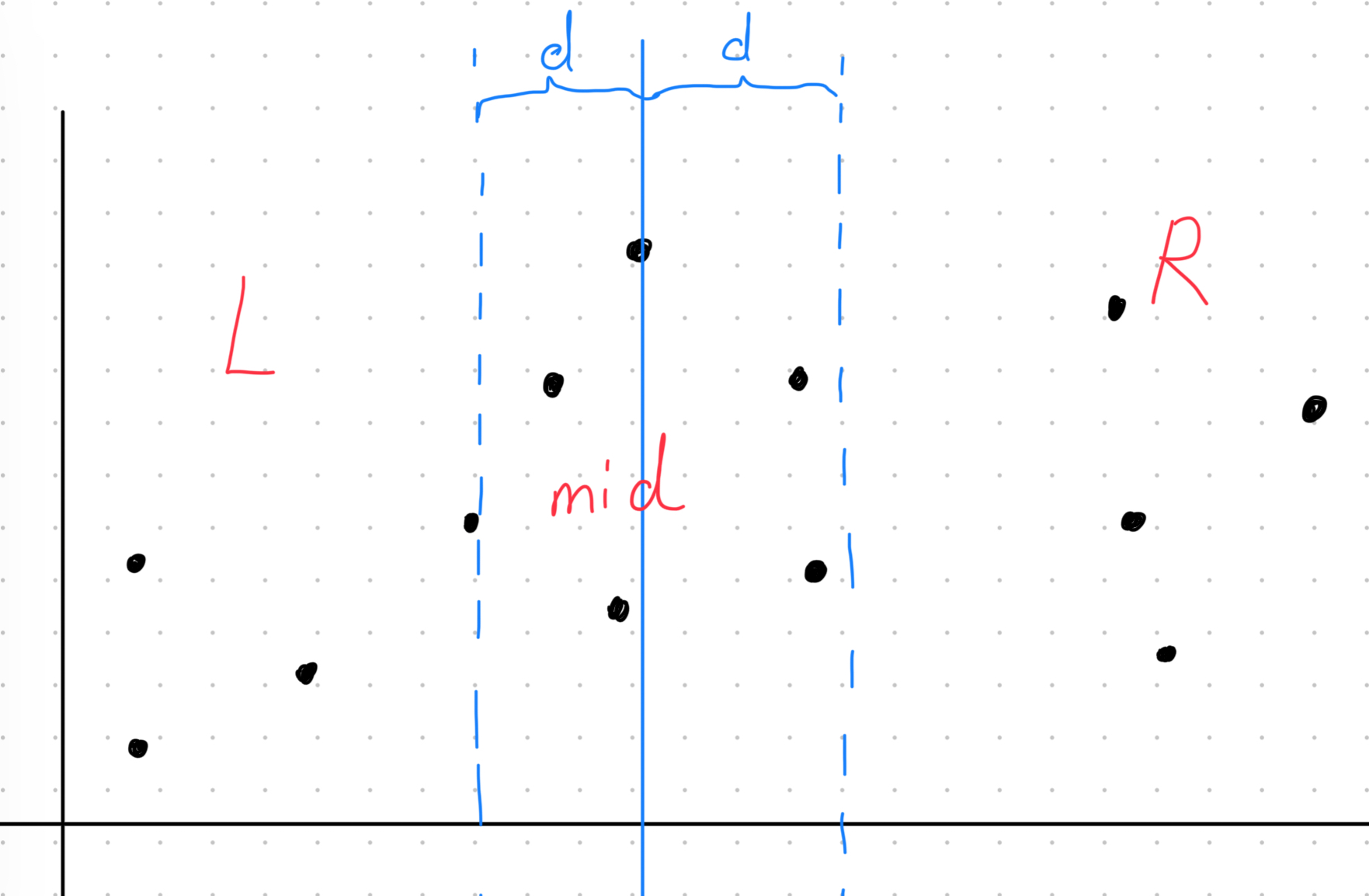
一道经典的分治题目链接 题意是套圈游戏要设计一款尺寸最大的圆环，满足圆环不会一次套中两个物品。每个物品有一个摆放坐标。我们要求的是这些物品中相邻最近的两个物品之间的距离，这个距离就是我们要求的圆环的直径。 这个类型网上常称为寻找最近点对问题。 ...

这是力扣上一道非常简单的问题，是经典的解决括号匹配问题。当然做法是用一个栈即可解决问题。有效的括号 这是我的代码：123456789101112131415161718192021222324class Solution { public boolean isValid(String s) { Stack<Character> st = new Stack(); boolean flag = true; for(int i=0;i<s.length();i++){ Character nowC = s.charAt(i); if(nowC=='('||nowC=='{'||nowC=='['){ st.push(nowC); }else { ...

博客的免费图床方案（Cloudflare R2 + PicGo）参考博客 这个博客写的已经非常详细清楚了，这里不再赘述实现步骤。 这里记录一下我是怎么发现这篇博客的。 在一个很无聊的时间段，我打开了Inoreader看RSS订阅的博客列表有没有更新，其中有一篇少数派的博客吸引了我，是这个博客。 这里博主提到了他的推特账号。其中很近的时间里他发布了上面提到的免费图床方案的博文。 这篇博客解决了我正在苦恼的问题，那就是博文中图片的插入。如果是只有一个github pages的静态网站还好说，直接传在相对文件夹里即可。但是如果面对多平台，比如我还想在csdn中发布，那就变得很麻烦，因为markdown里写的相对路径将不可用，最直接的办法就是更改每个图片链接。 然而如果是有自己的图床就很方便了，不用担心网络上的图片会突然失效，多平台发布也不用更改自己的截图路径。上方的图片就是用我自己实现的图库。 ...

正则表达式To the book page Regexp golf注意这里如果写对的话，应该什么都不会输出。 正则表达式中的\b是单词边界的标志，它用来匹配一个单词的边界。 123456789101112131415161718192021222324252627282930313233343536373839404142// Fill in the regular expressions// 正则表达式应该匹配“car”和“cat”，但不匹配其他字符串。verify(/ca[rt]/, ["my car", "bad cats"], ["camper", "high art"]);// 正则表达式应该匹配“pop”和“prop”，但不匹配其他字符串。verify(/pr?op/, ["pop culture", "mad props"], ["plop",...

使用高德SDK实现导航功能参考博客 Github仓库直达 这是今天企业实训的一个小作业，实际上我从昨天就开始尝试申请key然后下载官方Demo开始实验。本来是要做flutter项目，但是高德官方里flutter教程只有显示地图和定位功能，没有导航功能，导航功能官方只有Android的教程。今天也是用Android原生进行编写的。至于怎么整合到flutter项目里目前还不知道。。。 1. 官网下载SDK我也尝试过直接gradle引入包的操作，但是直接引入的会缺少AmapNaviParams。官网也一直强调有个什么东西开源了所以提供的包里移除了一些东西（不知道到底是什么）。 官网SDK下载地址 我下载的是导航合包： 2. 创建项目直接Android Studio创建一个java，Groovy的项目即可。 设置里需要设置生成所有Gradle Task： 这样你就可以靠点击这里直接获得你项目的SHA1的值，申请key的时候需要这个。 点击上图位置你就可以在终端看见你的SHA1值。在我这里release和debug的SHA1的值是一样的。 ...

错误To the book page Retry大概率触发MultiplicatorUnitFailure错误，承接直到运行成功并返回结果。 1234567891011121314151617181920212223242526272829class MultiplicatorUnitFailure extends Error {}function primitiveMultiply(a, b) { if (Math.random() < 0.2) { return a * b; } else { throw new MultiplicatorUnitFailure("Klunk"); }}function reliableMultiply(a, b) { // Your code here. for(;;){ try{ var ans = primitiveMultiply(a,b); ...

robotTo the book page代码解释由AI生成。 总代码数据结构和图的构建首先定义了村庄中各个地点之间的道路： 123456789const roads = [ "Alice's House-Bob's House", "Alice's House-Cabin", "Alice's House-Post Office", "Bob's House-Town Hall", "Daria's House-Ernie's House", "Daria's House-Town Hall", "Ernie's House-Grete's House", "Grete's House-Farm", "Grete's...

对象To the book page A vector type封装一个类，实现坐标的加减法，以及get属性的length返回坐标离原点的距离。 12345678910111213141516171819202122// Your code here.class Vec{ constructor(x,y){ this.x = x; this.y = y; } plus(other){ return new Vec(this.x+other.x,this.y+other.y); } minus(other){ return new Vec(this.x-other.x,this.y-other.y); } get length(){ return Math.sqrt(this.x**2+this.y**2); }}console.log(new Vec(1,...

高阶函数记录一下这本书的习题的答案，这是第五章的练习。 To the book page Flattening将包含数组的数组展开，即只有一对中括号的数组。 1234567let arrays = [[1, 2, 3], [4, 5], [6]];// Your code here.let combineArrays = arrays.reduce((accumulator,currentArray)=>{ return accumulator.concat(currentArray);},[])console.log(combineArrays);// → [1, 2, 3, 4, 5, 6] Your own loop如果不能满足条件（testAct）就不能继续循环。下一次循环要用新的值（updateAct），每次循环需要执行一定的操作（bodyAct）。 123456789101112// Your code here.function loop(value, testAct, updateAct,bodyAct){ ...

用Github Desktop简化你的推送流程Github Desktop官方网站 1. 第三方仓库克隆选择file->clone repository, 通过URL克隆你的仓库选择URL，里面填你的第三方仓库的https克隆链接，注意要填写公网地址而不是内网地址。 注意选择你保存仓库的本地位置 点击clone后应该会弹出让你输入用户名和密码，如果是gitlab，直接输入你登录gitlab的用户名和密码。 到此为止应该是可以克隆仓库到本地了。之后的操作，和一般的git操作是一致的，不过是有了图形化的界面，不用输入繁琐的命令。 2. add 和 commit直接到app界面，一旦仓库有文件更改，app界面会罗列出你更新文件的内容，需要你进行commit操作。 3. push处理完所有的commit后就可以进行推送了，直接点击界面右边的push origin 即可。